这是一篇CVX101的学习笔记, 5 duality一章的Geometric interpretation用图解的形式解读了一个problem的dual function, 并且用图解给出了在只考虑不等式约束条件下, strong duality的一个几何解释的充分必要条件, 以及一个充分条件: 在凸优化问题里的slater condition.

primal/dual problem的weak/strong duality的定义这里就不写了…

dual problem几何解释

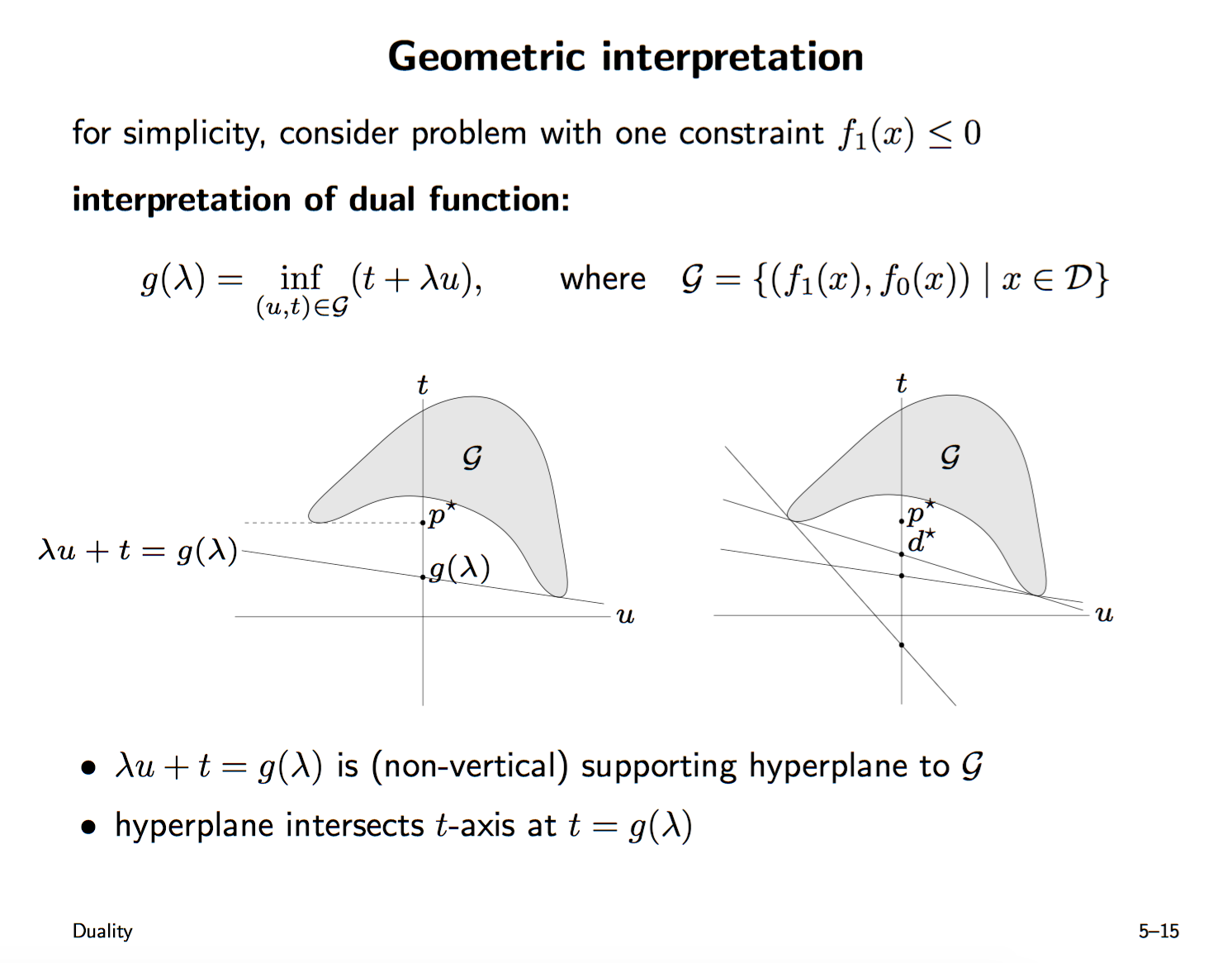
先看dual function $g(\lambda) = \inf_{x \in D} (f_0(x) + \lambda f_1(x)) = \inf_{(u, t) \in G} (t + \lambda u)$, 其中 $G = \{(f_1(x), f_0(x))

x \in D\}$

dual function相当于给定一个$\infty>\lambda>0$, 求一个以$(\lambda, 1)$为法线方向 且 刚好能和$G$相切的直线(supporting plane), 此时该直线和t轴的交点值为$g(\lambda)$。dual problem优化问题相当于找一个$\infty > \lambda > 0$, 使得该交点$g(\lambda)$越大越好. 可以看出上面slide1里举了一个存在duality gap的情况, 直观地看, 是因为$O$集合的非凸性, 使得不feasible区域里有些点干扰了我继续调整$\lambda$. $p^{*}$藏在了$G$的convex hull里. 我求切线也就是supporting plane的时候只能得到$G$convex hull的切线. 所以不能触碰到对应取到feasible的$f_0(x)=p^{*}, f_1(x) \leq 0$的$(f_1(x), f_0(x))$点。

回想之前也有类似的multi-criteria vector optimization的时候也做过类似的geometric interpretation, 当时要做的是优化一个向量的criteria $ f(x) = \begin{pmatrix} f_1(x)\\ f_2(x)\end{pmatrix} $. 其中如果要得到pareto optimal(minimal element of all possible criteria value set $O$, 即类似上面的$G$ set的minimal值), 一个经常的方法就是选一个scalarization, 选定一个$ \lambda >_{K^{*}} 0$, 求 $\lambda^T f(x)$在原约束上的scalar凸优化问题就可以得到一个原问题的pareto最优解($O$在凸问题上其lower-left part为凸的). 这个的几何解释就是一条法线为$\lambda$的直线与$O$相切的地方即为这个scalarized problem的最优解, 关于这个multi-criteria vector optimization的两页slides如下。可以看到优化这种形式$\lambda f_1 + f_0$的函数, $\lambda$在一次优化中给定, 都可以看作是multi-criteria vector optimization的一次scalarization, 那么就可以用这种切线/supporting plane的几何解释来理解!

在这个问题里, 要优化的是单个criteria, 但是Langranian multiplier从某种角度, 可以看作引入了又一个criteria. 其中拉格朗日乘子$\lambda > 0$类比为scalarized用的权重. 但是这里不一样的是, 我们的feasible point必须满足$f_1(x) \leq 0$, 而我们把$f_1(x)$作为一个criteria画出$G$的时候, $G$包括的点显然很可能有$f_1(x) > 0$。

strong duality的充要条件

在课程的前面我们看到这句话:

conditions that guarantee strong duality in convex problems are called constraint qualifications 其中slater condition / strengthened slater condition for linear inequalities是其中的一种constraint qualification.

从几何解释, 我们可能能推出一个更general的stong duality条件(虽然不一定好用于判定). 我们来看strong duality的充分必要条件是什么:

strong duality即可以用dual problem优化$\lambda$, 也就是优化直线的法线方向, 使得这个方向$G$的supporting plane和$t$轴的交点能刚好为$(0, p^{*})$

或者说能否有通过$(0, p^{*})$这个点是否有一个$G$的non-vertical($\lambda < \infty$) supporting plane.

虽然我们是从几何解释看出来这个定理的, 但是上面这个定理的充分性和必要性可以严格证明, 并不难, 可以参考一个notes)的第四章conditions for strong duality.

slater condition in convex problems

分析

定理里有两步, 一步是是否存在supporting plane, 另一步看是否为vertical. 下面我们想推一个对于凸优化问题的充分条件. 我们知道如果$G$是凸集, 那么肯定有supporting plane存在. 这和$G$的凸性有关, 而上即使$f_0(x)$, $f_1(x)$都是凸函数, $G$也不一定是凸集.

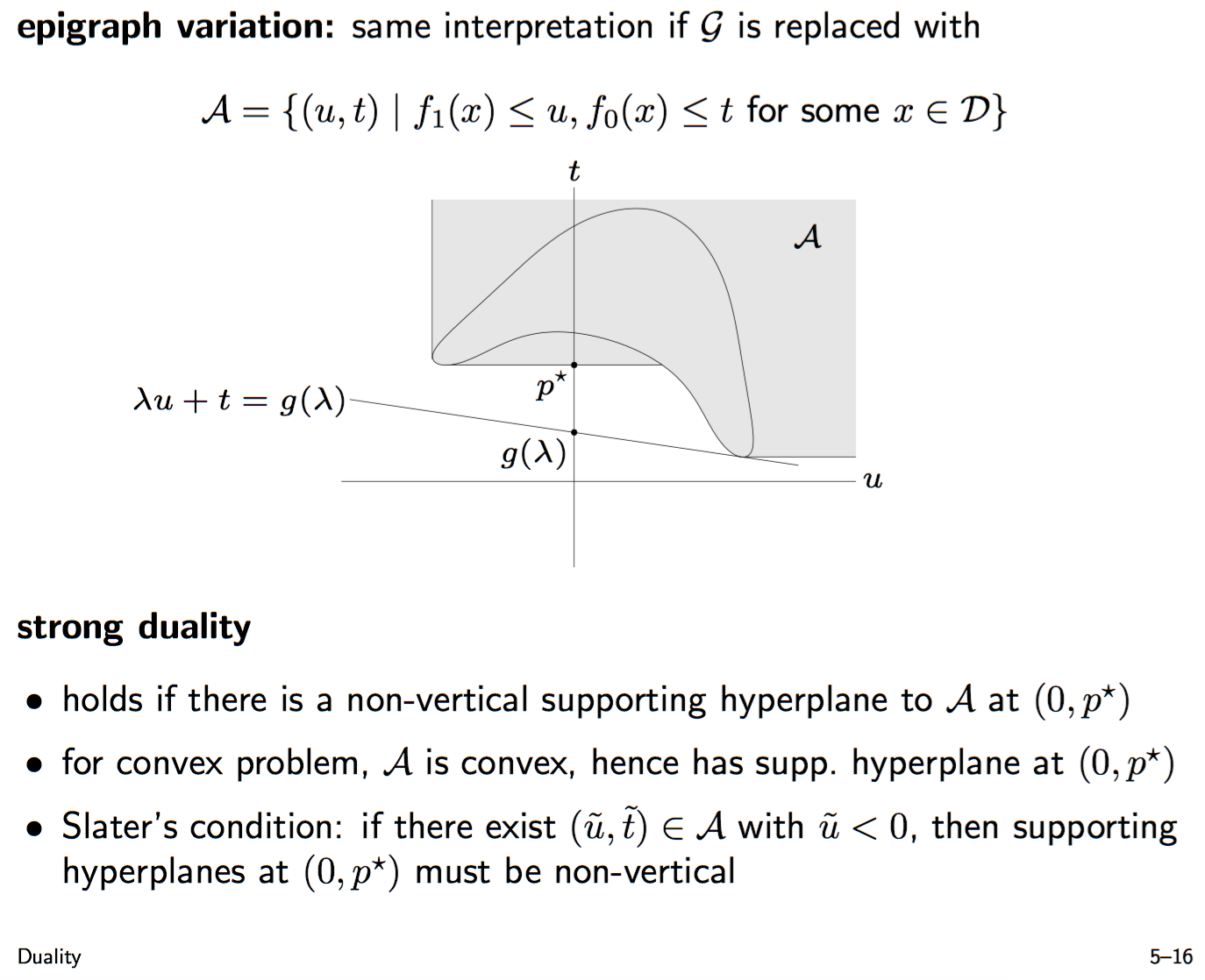
但是我们可以考虑$G$的一个epigraph variation. 因为虽然$\{(f_1(x), f_0(x))

x \in D\}$不是凸集, 但是向量函数$ f(x) = \begin{pmatrix} f_1(x)\\ f_0(x)\end{pmatrix} $对于2维postive orthant cone的generalized inequality一定是一个凸函数, 这个很明显因为每一维都是凸函数而相对postive orthant cone的generalized inequality就是每一维的scalar inequality. 我们知道一个凸函数的epigraph一定是凸集, 这里对于2dim generalized inequality的epigraph set显然是:

$$A = \\{(x, (u, t)) | \begin{pmatrix} f\_1(x)\\\\ f\_0(x)\end{pmatrix} \leq \begin{pmatrix} u\\\\ t\end{pmatrix}\\} = \\{(x, (u, t)) | f\_1(x) \leq u, f\_0(x) \leq t, x \in D\\}$$

NOTE: 时刻记住: 在这个对$G$或者$A$的分析中我们只考虑$x$的定义域(implicit/explicit), 还没有考虑feasible solution的问题!

我们知道$A$这个epigraph set of convex vector function为convex, 所以$A$在$(u,t)$两维度上的projection也为convex set。即$A = \{(u, t) | \exists x \in D, f_1(x) \leq u, f_0(x) \leq t\}$也为convex set。这个convex set画在图上就是slide2里面灰色区域的那样. 由$A,G$的定义分最优点$(f_1(x^{*}), p^{*})$在不在$f_1(x^{*}) = 0$的$t$轴上讨论, 可以看到几何解释中strong duality的充分必要条件对于$G$的supporting plane和对于$A$的是等效的. 所以:

strong duality holds if there is a non-vertical supporting hyperplane to A at (0, p*)

slater condition

下面来看strong duality的一个充分条件: slater condtion.

slater condition说的: convex problem且有着strict feasible interior满足$\exists x \in D, \mbox{ s.t. } f_1(x) < 0$.

如果是convex problem, 我们已知$A$是convex的,那么在所有$A$的边界点肯定都有supporting plane(supporting plane theorem of convex set), 那么只要满足non-vertical就肯定strong duality了。$A$是凸集过$(0, p^{*})$, 只要在$t < 0$区域里有一个点$V$, 则在$(0, p^{*})$点的supporting plane一定不会是vertical的.

如果是 vertical, 那么要么该点$V$和凸集$A$中其他部分在supporting plane的两边(违背凸集定义, 或者也可以通过$(0, p^{*})$和$V$构造中间点违背凸集性质)要么$p^{*}$不为最优值(与假设矛盾).

画出图很好理解(一般构造性的证明也可以借助画图来想). 这就说明了slater condition在凸问题情况下是strong duality的充分条件。

KKT条件

下一步, 如果strong duality满足, 通过很简单的推导就可以得: 如果$f_i, h_i$可微, primal problem和dual problem的最优对$x^{*}, (\lambda^{*}, v^{*})$一定满足KKT条件。KKT条件其实就是

• primal constraints
• dual constraints
• complementary slackness
• gradient of Lagranian respect to $x$ equals zero: $\nabla_x L(x, \lambda, v) = 0$

来看converse的命题满不满足, 如果某个$\tilde{x}, (\tilde{\lambda}, \tilde{v})$对满足KKT条件, 是否为optimal, 且是否满足strong duality?

可以看到, 如果问题为convex问题的话. 如果第四条condition满足那么根据convex 函数性质, 一定有: $L(\tilde{x}, \tilde{\lambda}, \tilde{v}) = \inf_{x} L(x, \lambda, v) = g(\tilde{\lambda}, \tilde{v})$. 又由于complentary slackness, 可以得到strong duality满足. 如果对于这对pair storng duality都满足了, 那当然这对值$\tilde{x}, (\tilde{\lambda}, \tilde{v})$就是原问题和对偶问题的最优值(因为下界关系lower bound property).

所以对于凸优化问题, 有pair满足KKT条件是这个pair为optimal和strong duality的充分必要条件。

我们知道无约束可微凸优化问题, optimal值充分必要条件就是第四条gradient等于0。所以可以把KKT条件看作对于有约束可微凸优化问题的对gradient条件的扩展, 有意义的扩展其实是第三条: complementary slackness(因为前两条就是constraint嘛).

这里的例子课程中举的是walter filling问题(其总结待续).

dual problem在实际问题中的应用

• weak duality property: 从实际应用角度, 对于很多迭代优化算法, dual problem提供了一个原问题解的parametrized lower bound, 所以提供了一个算法迭代中止条件(stopping criterion): 找到一个$\lambda, v$得到$g(\lambda, v)$, 如果局部迭代优化算法得到的$f(x) - g(\lambda, v) < \mbox{epsilon}$, 一定有$f(x) - f^{*} < \mbox{epsilon}$.

• perturbation sensitivity analysis: dual problem解出对于各个不等式约束的最优Lagranian系数$\lambda_i$是否为0反映了对应的不等式约束$f_i$是否tight, 如果tight即$\lambda_i \neq 0$, $\lambda_i$越大说明对应的约束更tight, 如果这个约束被缩紧, 问题的最优解肯定会有越大的degration(NOTE: converse direction is not true globally, only locally… sad).